【点云局部特征描述子】PFH & FPFH

初晴天

1. 前言

点云局部特征描述子（3D Local Feature Descriptor）对于物体识别（Object Recognition）、点云配准（Registeration）、模型检索（Model Retrieval）等应用具有重要的意义。虽然，近几年深度学习“大行其道”，各种基于数据驱动的描述子开始涌现，但传统的 hand-crafted 特征还是值得学习与借鉴。
PFH 和 FPFH 是 PCL 库的作者 Radu Bogdan Rusu 博士提出的，相关论文如下：

• PFH：Aligning point cloud views using persistent feature histograms. IROS, 2008.
  
• FPFH：Fast Point Feature Histograms (FPFH) for 3D registration. ICRA, 2009.
  
• Rusu Dissertation：Semantic 3D Object Maps for Everyday Manipulation in Human Living Environments. 2009.
  

2. Point Feature Histograms (PFH)

2.1 原理

PFH 特征描述是基于特征点（keypoint）与其邻域点的空间几何关系来编码的。如图1所示，中间红色的特征点作为 query point，在其邻域（指定半径）内搜索 k 个点（蓝色），对于query point 和 k-neighbors 这 k+1 个点，两两配对，可以得到 k(k+1)/2 个点对（point pair）。



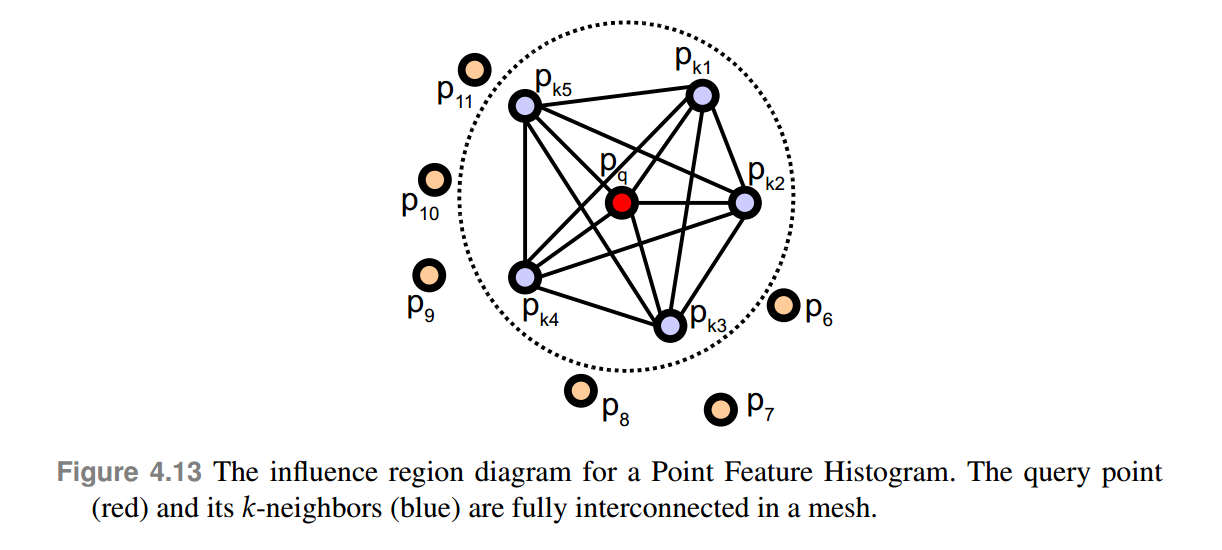
图 1

（1）构建点对坐标系（Pairwise Local coordinate）
对于每一组点对，首先建立局部坐标系：
\begin{align} u &= n_s \\ v &= u\times\frac{(p_t-p_s)}{||p_t-p_s||^2} \\ w &= u \times v \\ \end{align} \\
其中， \times 表示外积。
注意：这里的局部坐标系的概念与 Point Pair Feature（PPF）中的类似，是对关键点支撑区域中的每个点对（point pair）构建的，这是为了计算后面的角度特征；但是，其不同于 SHOT 描述子中的 Local Reference Frame（LRF），在关键点支撑区域（spherical support）内只构建一个 LRF（unique，invariant to rotation, repeatable），基于 LRF 对支撑区域进行特征提取。
（2）特征描述
基于其特征表示为：
\begin{align} \alpha &= v \cdot n_t \\ \phi &= u \cdot \frac{(p_t-p_s)}{d} \\ \theta &= arctan(w\cdot n_t, \ u\cdot n_t) \\ d &= ||p_t-p_s||_2 \\ \end{align} \\
其中， \cdot  表示内积，d 为 source point 和 target point 的欧式距离。



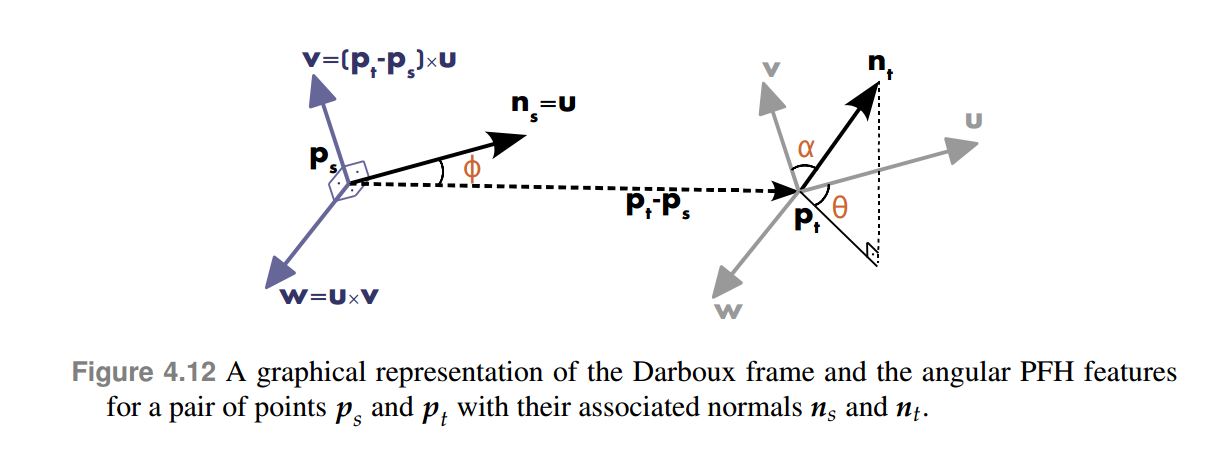
图 2

（3）特征编码
为了计算查询点 p_i 的 PFH 特征，将其邻域 k(k+1)/2 个点对的 quadruplets <\alpha, \phi, \theta, d> 特征集合放在一个直方图中，统计投票数量。具体而言，将每个特征划分为 n 个区间，则 PFH 特征矢量有 n^4 维。前三个特征都为角度，因此可以做归一化处理。



图 3

2.2 PCL 实现

PCL 中 FPH 的实现只取了前三个角度特征，将每个角度特征划分为 5 个 binning subdivisions，因而特征矢量有 125 维（pcl::PFHSignature125）。
#include <pcl/point_types.h>
#include <pcl/features/pfh.h>

typedef pcl::PointXYZ PointT;
typedef pcl::PointCloud<PointT> PointCloudT;
typedef pcl::Normal NormalT;
typedef pcl::PointCloud<NormalT> PointCloudNT;

{
  // 输入点云及其法向量，也可以直接输入带法向量的点云
  PointCloudT::Ptr cloud (new PointCloudT);
  PointCloudNT::Ptr normals (new PointCloudNT);

  // 创建 PFH 描述子
  pcl::PFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::PFHSignature125> pfh;
  pfh.setInputCloud (cloud);
  pfh.setInputNormals (normals);
  // 如果输入的是带法向量的点云，可以直接输入 pfh.setInputNormals (cloud)

  // 创建 kdtree
  pcl::search::KdTree<PointT>::Ptr tree (new pcl::search::KdTree<PointT>);
  pfh.setSearchMethod (tree);

  // 定义输出
  pcl::PointCloud<pcl::PFHSignature125>::Ptr pfhs (new pcl::PointCloud<pcl::PFHSignature125> ());

  // 设置搜索球半径 5cm
  // 注意！！这里的半径必须大于法向量估计时的半径
  pfh.setRadiusSearch (0.05);

  // Compute the features
  pfh.compute (*pfhs);

  // pfhs->points.size () should have the same size as the input cloud->points.size ()*
}
若要求 PFH 描述子，可以通过下面的函数实现：
template<typename PointInT, typename PointNT, typename PointOutT >
bool pcl::PFHEstimation<PointInT, PointNT, PointOutT>::computePairFeatures(       
            const pcl::PointCloud<PointInT> & cloud,
            const pcl::PointCloud<PointNT> & normals,
            int p_idx,  // the index of the first point (source)
            int q_idx,  // the index of the second point (target)
            float & f1, // angle between the projection of nq_idx and u
            float & f2, // angle between nq_idx and v
            float & f3, // angle between np_idx and |p_idx - q_idx|
            float & f4  // the distance feature (p_idx - q_idx)
)       
若 k 邻域已知，则可以通过下面函数来计算 PFH 特征描述子：
template<typename PointInT, typename PointNT, typename PointOutT>
void pcl::PFHEstimation<PointInT, PointNT, PointOutT>::computePointPFHSignature(       
          const pcl::PointCloud<PointInT> & cloud,
          const pcl::PointCloud<PointNT> & normals,
          const std::vector<int> & indices, // k 近邻点集合
          int nr_split,                     // 表示 bins 的数量
          Eigen::VectorXf & pfh_histogram   // 输出的特征描述子
)       
注意：为了计算效率，PFHEstimation 默认没有检查法向量是否包含 NaN 或 infinite value，所以在调用 complete() 函数之前需 check 一下：
for (int i = 0; i < normals->points.size(); i++)
{
  if (!pcl::isFinite<pcl::Normal>(normals->points))
  {
    PCL_WARN("normals[%d] is not finite\n", i);
  }
}
3. Fast Point Feature Histograms (FPFH)

3.1 原理

对于一个查询点，计算 PFH 特征的时间复杂度为 O(k^2) ，若一个点云有 n 个点，则时间复杂度为 O(nk^2)，效率非常低。因而，Rosu 博士在保留 PFH 核心思想上提出了 Fast PFH（FPFH）特征描述子，将计算复杂度将为 O(nk)。具体而言：
（1）将 <\alpha, \phi, \theta, d>特征简化为 <\alpha, \phi, \theta>，这称为 Simplified Point Feature Histogram (SPFH)；
（2）修正了 k 邻域点对的统计方式，分为两部分：一部分是查询点 p_q 与周围 k 个点组成的点对，另一部分是每个邻点与周围 k 个点组成的点对，第二部分的统计量取加权平均，如下式：


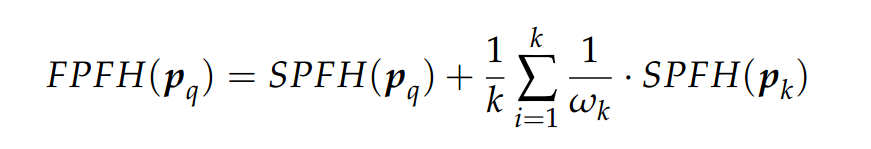
其中，权重 w_k 表示查询点 p_q 与邻点 p_k 的距离。这将搜索空间扩大到最多 2r 的范围。
（3）PFH 的特征空间是 fully correlated，假如有3个角度特征，每个特征分为5份，则有 5^3=125 维，可以用一个 5\times5\times5 的立方体格子来描述，每个小格子同时对应着三个特征。这种描述方式会造成很多小格子中的值为0，有点 redundant，不够 compact。一种简化的方法是直接将三个特征的特征矢量线性连接在一起，因而有15维。



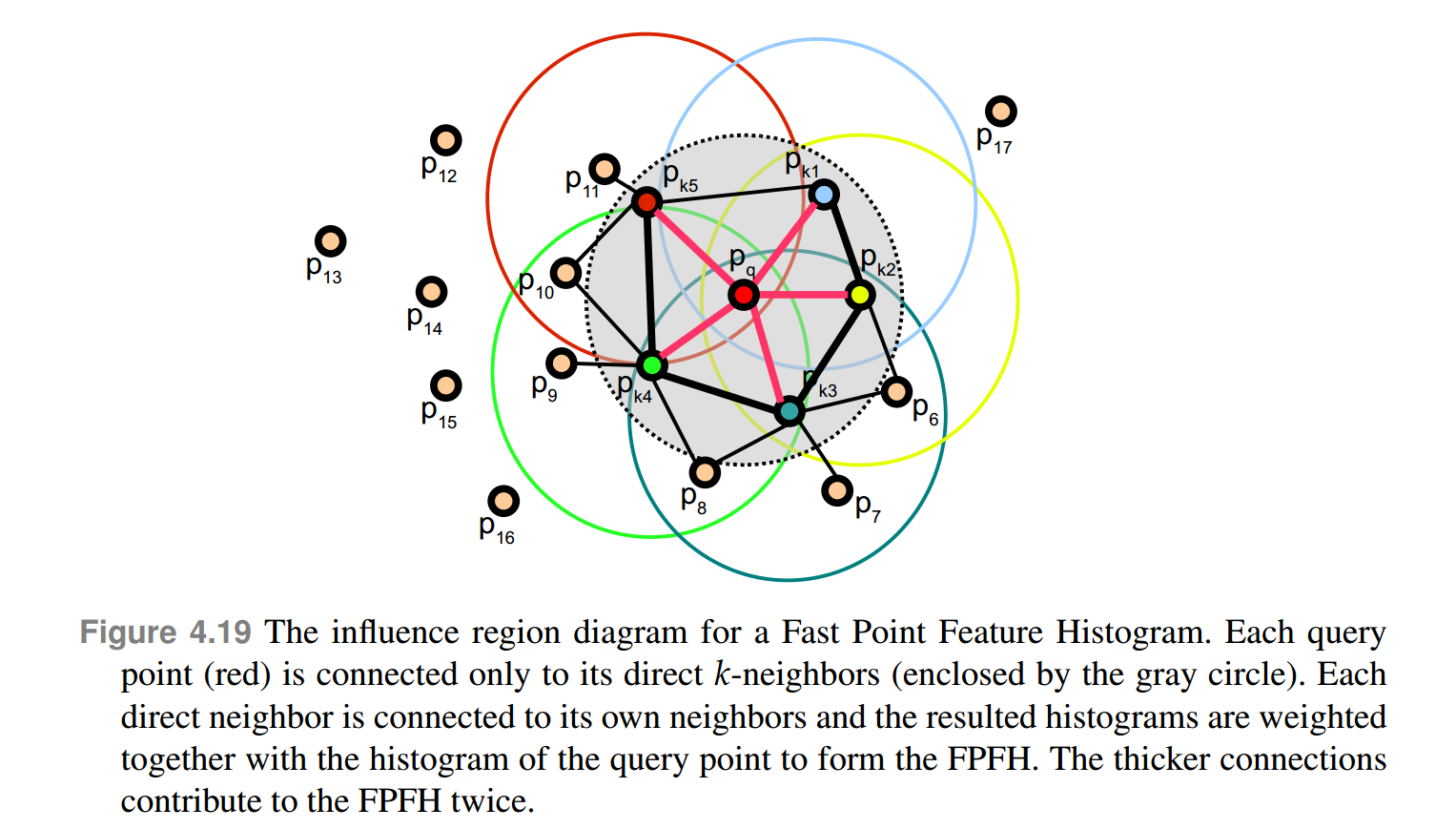
图 4

FPFH 特征的计算流程如下图所示。



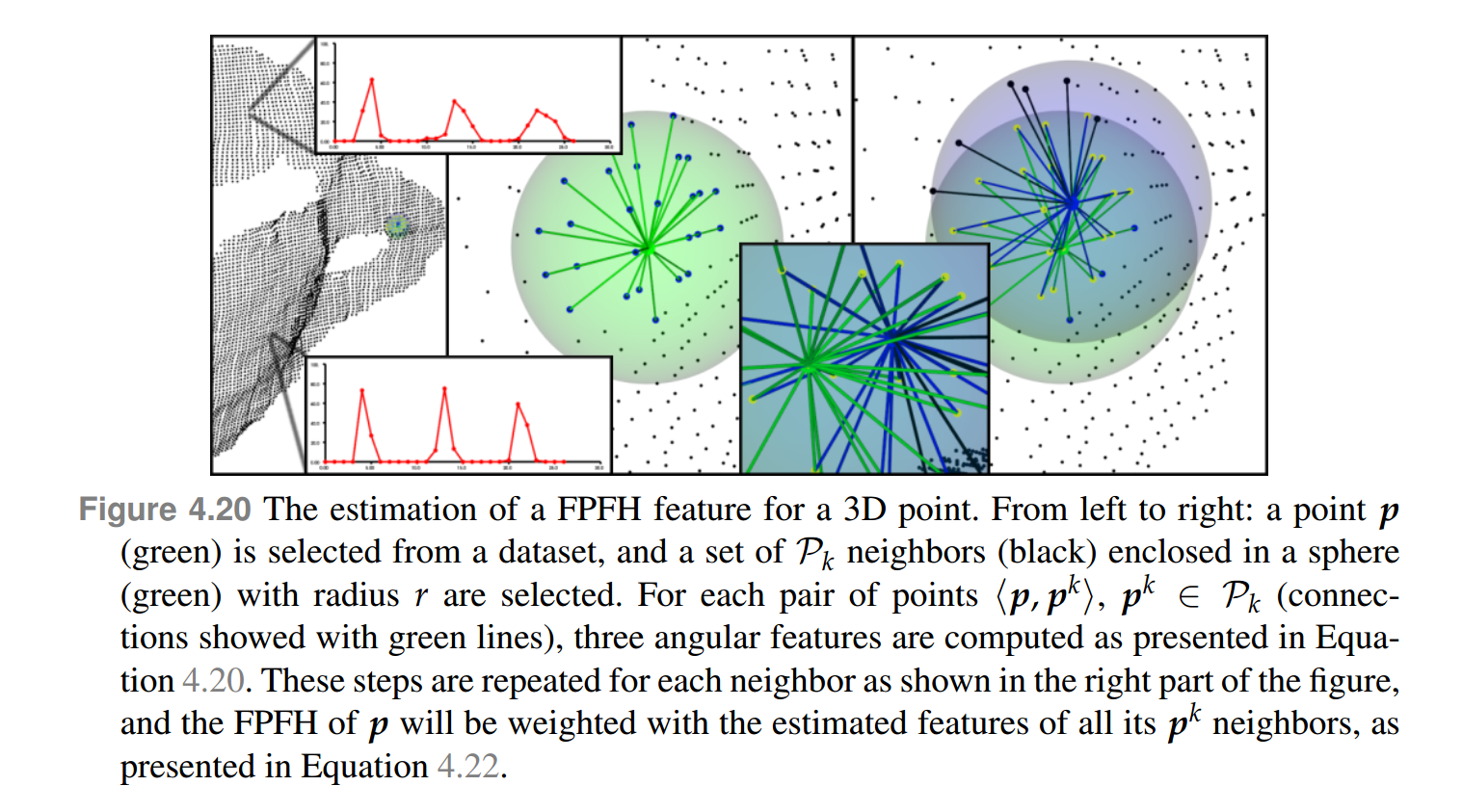
图 5

3.2 PCL实现

PCL 将三个角度特征中的每一个划分为 11 等份，因而特征矢量有33维，描述子pcl::FPFHSignature33，如下。
#include <pcl/point_types.h>
#include <pcl/features/fpfh.h>

{
  // 创建 FPFH 描述子
  pcl::FPFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::FPFHSignature33> fpfh;
  
  // 定义输出
  pcl::PointCloud<pcl::FPFHSignature33>::Ptr fpfhs (new pcl::PointCloud<pcl::FPFHSignature33> ());
}
PCL还实现了 OpenMP 加速的版本：pcl::FPFHEstimationOMP，在8核的机器上，可以加速6-8倍。
FPFH 特征直方图可视化：



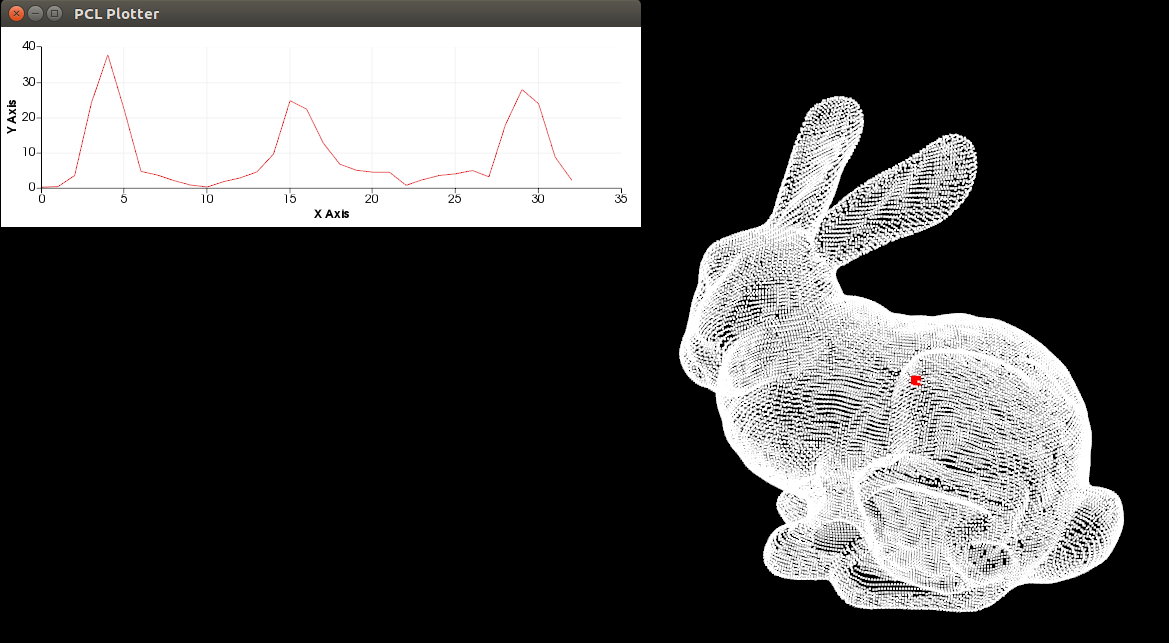
图 6

国米老当家

你好，我想请教个问题，FPFH可以用来做二维粗配准吗

骚

您好，我想请教一下，假如FPFH有三个角度特征，每个特征分为11份，为什么合在一起后就是33份了，这里该怎样理解呢

鸽子樹

直接 concatenate 在一起

范波

您好，想请教一下为何每个特征要分为11份，是根据经验取的这个数吗，另外想请教一下为何要选取那三个角度作为特征呢？

海浪星体育

1.红色的特征点作为 query point，在其邻域（指定半径）内搜索 k 个点（蓝色），对于query point 和 k-neighbors 这 k+1 个点，两两配对，可以得到 [公式] 个点对（point pair）。----原文是for each point p, all of p’s neighbors enclosed in the sphere with a given radius r are selected ，所有点，不是任意K个点。

2. 特征编码没讲：

雪花漫飞

我觉得可以

奔雷手

[图片]

草帽海贼

终于有文章说SPFH是啥了，真难找

去宁马蛋

你好，原论文那三个角度除了最后一个角度，其余两个都是角度的余弦，并不是角度，为什么全网都用角度来表示，而没有人提及余弦呢，而且原文用的是f1 f2 f3 f4