|
|
上一篇文章介绍了差分的定义以及如何使用,这篇文章将继续介绍二维差分的使用。
2.二维差分
2.1. 定义
对于一个给定的矩阵 A ,它的差分矩阵 B 中 B_{i,j} 可用如下公式计算:
B_{i,j} = A_{i,j} - A_{i-1,j} - A_{i,j-1} + A_{i-1,j-1}, (1 \leq i \leq n) \\ 实际上,上面的公式更像是通过原矩阵是差分矩阵的前缀和这个条件推导出来的,因此,不像一维差分定义那样直观。
(一维差分的定义:表示原数列中两个相邻元素的差)。
这里不用过于纠结二维差分矩阵的定义,后面我们也会给出其他方式来生成差分矩阵,而不用根据定义来推导。
一维差分与二维差分的关系如下图所示:
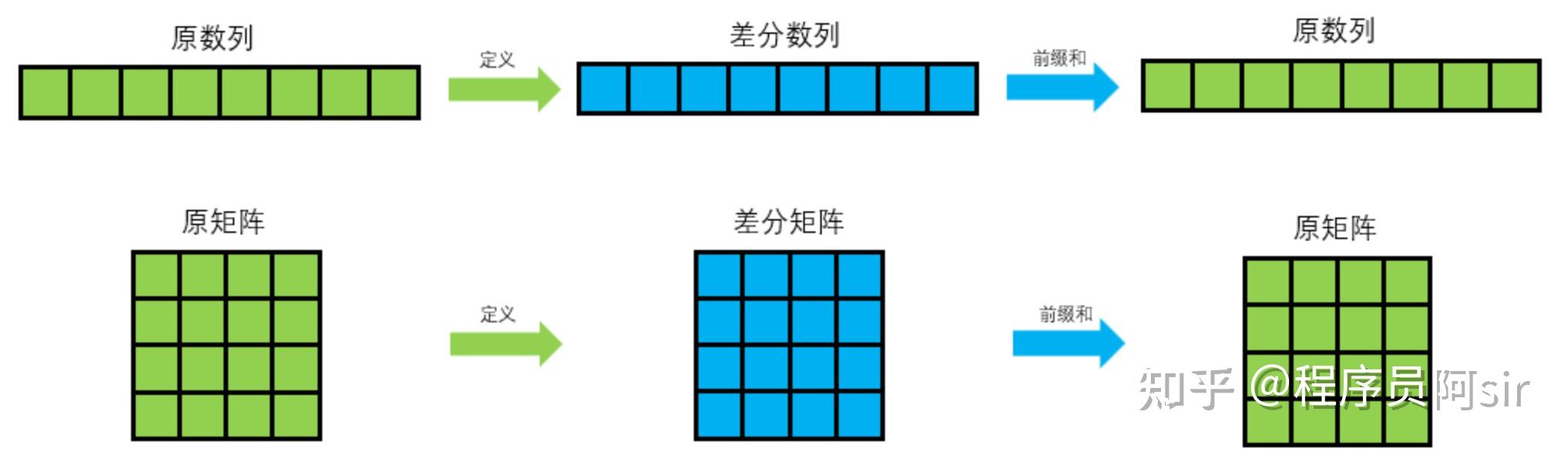
一维差分与二维差分的对应关系
2.2. 如何使用
结合前面文章中差分的用途,可以容易的想到,二维差分主要是用于快速将一个区块中的所有元素都加上 d。
如下图所示。
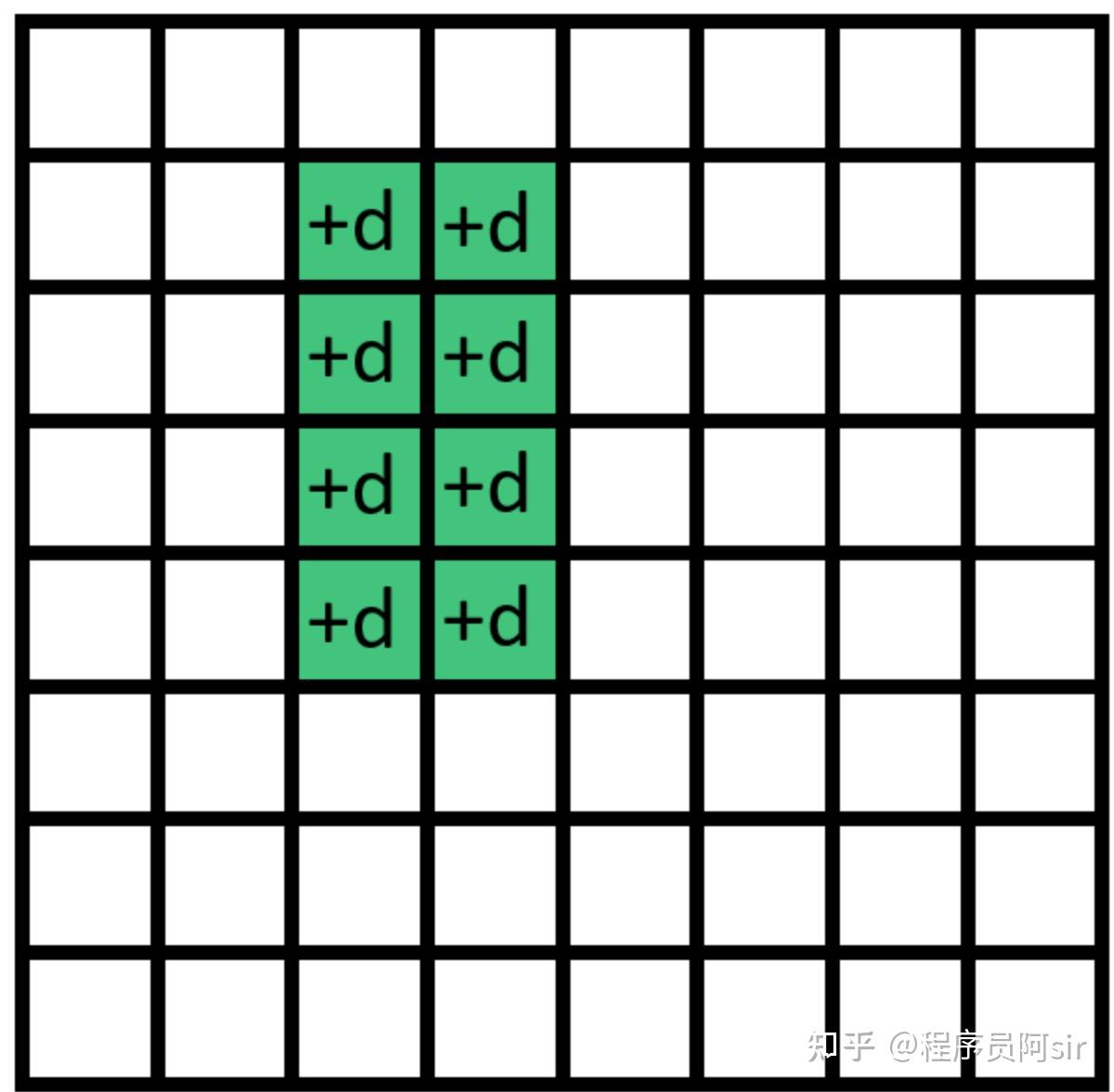
二维差分用途
假设:原二维数组是 A,其差分矩阵是 B,矩阵维度为 (n, m),即左上角元素下标为 (1,1),右下角元素下标为 (n, m)。
那么对差分矩阵中下标为 (i,j) 的元素加上 d 等价于对原矩阵中,以 (i,j) 为左上角,以 (n, m) 为右下角的区块每个值加上 d。
因为原矩阵 A 是差分矩阵 B 的前缀和。
假设把 B 中 (x, y) 下标的点加上 d,那么算前缀和时,只要经过该点,那前缀和都会加上 d。
而 (x,y)右下方的所有点表示的前缀和都会经过 (x,y) 。
(因为二维前缀和是计算矩阵左上方所有元素的和)。
所以:
对差分矩阵中下标为 (i,j) 的元素加上 d 等价于对原矩阵中,以 (i,j) 为左上角,以 (n, m) 为右下角的区块每个值加上 d。
结合下图可能更容易理解:
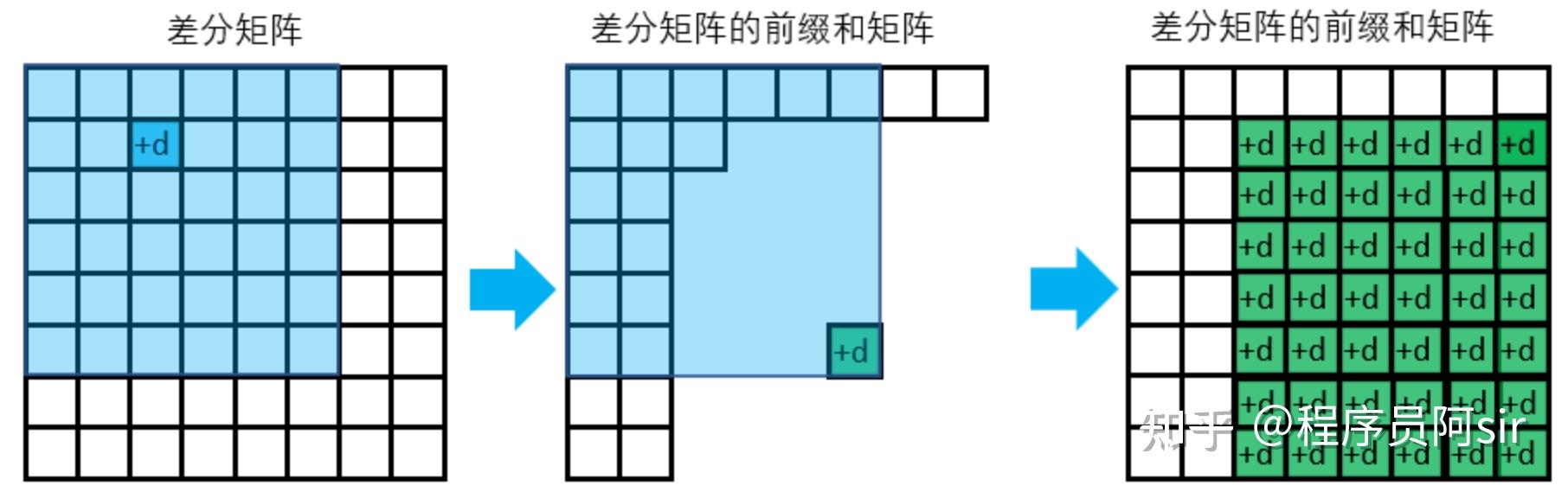
差分矩阵修改对应到原矩阵的修改示例
上图,左边表示差分矩阵,右半边表示差分矩阵的前缀和矩阵,也就是原矩阵。
图中展示了差分矩阵中某个元素加上了 d,那其前缀和矩阵中绿色位置的前缀和就是差分矩阵中蓝色阴影部分的总和。
蓝色阴影部分只有蓝色块位置加上了 d,因此其前缀和矩阵中绿色位置元素也加上了 d。
所以,就有了最右边的图中前缀和矩阵的右下角每个元素都加上了 d。
因为差分矩阵的前缀和矩阵就是原矩阵,因此可以得出上面的结论。
现在考虑如何将上述操作转化为对差分矩阵的单点操作。
先说结论:
假设:区块左上角下标为 (x_1, y_1),右下角下标为 (x_2, y_2)。
对 A 矩阵中该区块的每个元素都加上 d 的操作等价于进行下面四个操作:
B[x_1, y_1] += d \\ B[x_2+1, y_1] -= d \\ B[x_1, y_2+1] -= d \\ B[x_2+1, y_2+1] += d \\ 这里,由于篇幅原因不再详细解释了,相信大家根据前面介绍前缀和的文章中讲的二维前缀和计算方法以及上面介绍的差分矩阵修改与原矩阵之前的对应关系,可以轻松理清上面的公式。
但除此之外,还有一个问题没有解决:
如何计算差分矩阵?
因为如果我们想通过差分矩阵将区块操作转化为单点操作,首先要有差分矩阵。
通过上面的定义可以计算,但是需要记住公式,比较复杂。
这里介绍一种比较巧妙的方法:将差分矩阵中每个元素一个一个的插进去。
下面具体说明:
首先假设原矩阵 A 是全 0 矩阵,那其差分矩阵 B 显然也是全 0 矩阵,这样完全符合定义。
接下来将 A 中每个元素依次更新为实际值。
例如:题目中原矩阵的第 (2,8) 个位置应该是 5,那相当于将原矩阵以 (2,8)为左上角,同样以 (2,8)为右下角的所有元素加上了 5。
于是,便可以转化为四个操作:
B[2,8] += 5 \\ B[3,8] -= 5 \\ B[2,9] -= 5 \\ B[3,9] += 5 \\ 这样,当原矩阵中每个元素都这样插入完,原矩阵就符合题意了,也顺便得到了整个差分矩阵。
2.3. 模板
例题:ACWing 798. 差分矩阵
题目描述:
输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
输入格式:
第一行包含整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含 5 个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式:
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵 代码实现模板:
void insert(int x1, int y1, int x2, int y2, int d)
{
b[x1][y1] += d;
b[x2 + 1][y1] -= d;
b[x1][y2 + 1] -= d;
b[x2 + 1][y2 + 1] += d;
}
int main()
{
int n, m, q;
scanf("%d%d%d", &n, &m, &q);
// 输入原矩阵,并依次构造差分矩阵
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
scanf(&#34;%d&#34;, &a[j]);
insert(i, j, i, j, a[j]);
}
while (q--)
{
int x1, y1, x2, y2, d;
scanf(&#34;%d%d%d%d%d&#34;, &x1, &y1, &x2, &y2, &d);
insert(x1, y1, x2, y2, d); // 差分矩阵操作
}
// 计算差分矩阵的前缀和,也就是原矩阵的新值
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
a[j] = a[i - 1][j] + a[j - 1] - a[i - 1][j - 1] + b[j];
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
printf(&#34;%d &#34;, a[j]);
}
printf(&#34;\n&#34;);
}
return 0;
}
总结
差分: 主要用于把对一个区间的操作转化为对左右两个端点元素的单点操作,再通过前缀和得到原问题的解,以此降低求解难度。
二维差分的初始化可以通过从全0矩阵构造的方法来获取,这样就巧妙地避开了直接通过数学定义计算差分的过程。
其实一维差分也可以通过这种方式来构造,相信大家已经很容易理解了。
参考资料
|
|