|
|
写在前面
- 现实世界的复杂性使得自动控制系统运行时面临着各种各样的干扰,如环境对控制系统施加的影响、设备本身的非理想特性造成的干扰,这些干扰的存在使得控制系统的表现脱离预期,因此,干扰衰减/抑制(Disturbance Rejection/Attenuation)成为控制系统设计的一个永恒主题。如果干扰已知或者可以测量,且进入系统的方式比较明确,自然可以通过前馈消除。对于干扰未知,但是有上界的情况来说,滑模控制SMC(Sliding mode control)通过在滑模面上的高频切换,在时间平均意义上实现了对未知干扰进行有效逼近和补偿。(具体分析可以参考‘控制算法手记-滑模控制滑的是什么模’)。对于未知干扰,如图1所示,干扰观测器(Disturbance Observer)提供了另一种解决问题的思路:当干扰存在并与控制输入一起进入被控系统时,导致系统输出相比无干扰情况发生偏离;那么,将控制输入、受到干扰偏离的控制输出与无干扰时被控对象模型(即名义/标称/Nominal 模型)提供的信息相结合,应该能够反算出未知干扰。与状态观测器不同的是,形式上,这里的干扰是独立于系统状态之外的信号(干扰动态模型未知)。为限定讨论范围,其他形式的干扰观测器如滑模、ESO(将干扰扩张成附加的系统动态,且误差由观测输出误差驱动)等暂不在本文讨论范围(感兴趣的朋友可以参考参考文献【1】~【4】)。
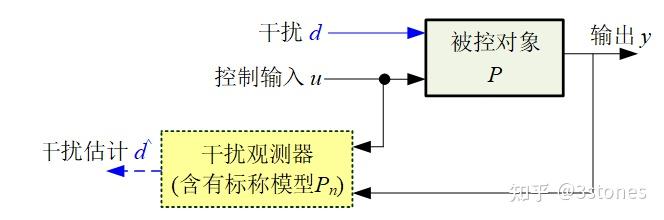
图1. 干扰观测器DO的基本原理
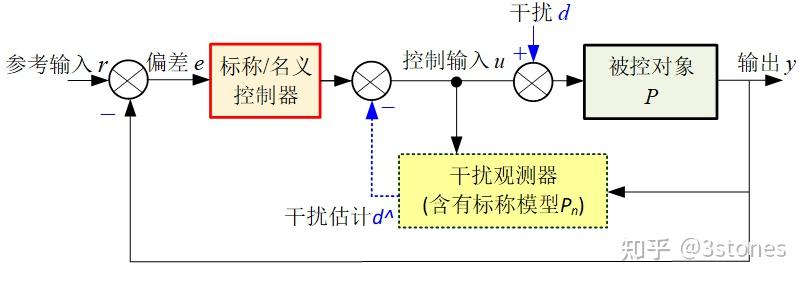
图2. 基于干扰观测器的控制DOBC的基本原理
- 如图2所示,DO的引入为基于干扰观测器的控制DOBC(Disturbance-Observer based Control)奠定了基础。类似于前馈控制,DOBC在二自由度控制系统的架构下(具体可参考‘控制算法手记-二自由度控制器’),将观测到的未知干扰在控制输入端进行前馈补偿(控制输入和未知干扰进入系统在同一通道,即匹配性干扰/Matched Disturbance可以直接补偿,运动控制系统中,干扰多为外界负载或者摩擦力,控制输入为力/力矩时,则为匹配干扰,控制输入为电压时,则为非匹配干扰/Unmatched Disturbance),从而减小或者消除未知感染对系统的影响。DOBC使得控制系统的设计能够兼顾跟踪与抗扰性能、名义/标称性能与鲁棒性能。DO可以作为单独附加模型(Stand-alone Add-on Module)整合到原有控制系统中,从而改进控制性能的优势,在实际中得到了广泛应用。
- DOBC本质上也是一种基于(机理)模型的控制方法,建立合适的被控系统(名义/标称/Nominal)模型是成功运用该方法的第一步。应该注意到任何模型都是对被控系统的近似描述,无论形式如何(传递函数、状态方程),这种描述都应该抓住问题的本质或者主要矛盾。在干扰观测器的语境下,系统模型包含标称模型和干扰两部分,没有被标称模型描述的,并对控制性能/输出有影响的都可以被认为是干扰(对于同一个被控对象,标称模型不同,控制算法设计语境下的干扰定义也随之变化)。这种分离处理方法相比其他鲁棒性控制算法简化了控制器的设计过程:针对干扰,设计干扰观测器观测干扰,并在输入端进行补偿,完成补偿后,可以忽略干扰对控制系统影响;针对标称模型所描述的动力学行为,再设计相应的标称控制器(Nominal controller)使得标称模型对应的动力学行为和标称控制器组合形成控制系统行为符合期望。
- 如上所述:标称模型的选取和建立、干扰观测的方法以及针对标称模型的标称控制器设计构成了DOBC的主要组成部分,实际上这也DOBC在形式上区别不同干扰观测器控制方法的主要依据。比如对于ADRC(自抗扰控制器)和ESO(扩展状态观测器)来说,标称模型就是积分串联型,干扰观测方法就是利用伦贝格观测器(Luenberger Observer)的思路估计扩张成额外状态的总扰动;滑模干扰观测器则利用滑模设计思路能够有效时间内收敛的优势进行干扰估计,标称模型可以认为和DOBC相差不大。这两种干扰观测器一般都在状态空间模型下进行设计,对于线性系统,DOBC则可以在传递函数的架构,利用标称模型的逆(inverse nominal model)下进行。
- 干扰观测器DO同H无穷、滑模控制类似,是一种鲁棒控制方法,自上世纪80年代由日本学者Ohnishi提出以来[4],在运动控制系统中得到了广泛应用,如多关节机器臂控制、机器臂遥操作(Tele-operation)控制、工业伺服电机、车辆运动控制、飞行控制系统以及精密运动控制系统。在这些应用场合中,未知摩擦力/负载力、控制系统本身的参数变化都是影响控制性能的主要因素。对于过程控制(Process Control),目前以仿真研究较多,实验验证或者已经工业应用案例相对较少。在DOBC应用过程中,干扰是否匹配输入(Matched/Unmatched disturbance),被控对象本身的特性(不稳定零点/非最小相位系统标称模型求逆),传感器噪声和信号传输延迟、滤波设计等问题仍是需要特别关注的问题。
根据被控系统是线性或者非线性,DO可以分为线性观测器LD0和非线性观测器NDO,本文将主要围绕LDO进行介绍。
线性干扰观测器LDO原理
对于线性被控系统,DO的分析和设计通常在频域进行,如图3所。对于单输入单输出非最小相位系统而言(无不稳定的零点和极点),LDO一般包含逆标称模型和滤波器Q(s),根据输出信号y、测量噪声n,和控制输入u, 估计出外界干扰d^,嵌入到系统内部环路中,与外环控制器C(基于名义/标称模型Pn设计)一起,组成整个控制回路。为简明起见,表1给出了引入LDO前后的传递函数对比。
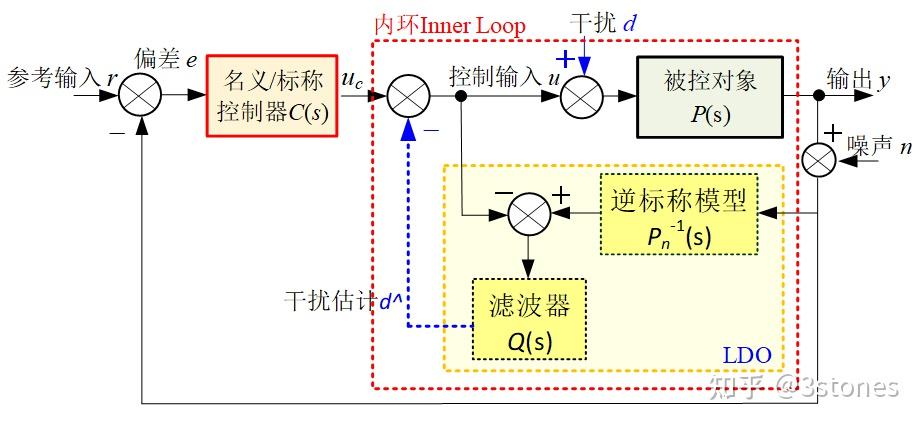
图3. 线性干扰观测器LDO及其控制系统LDOBC
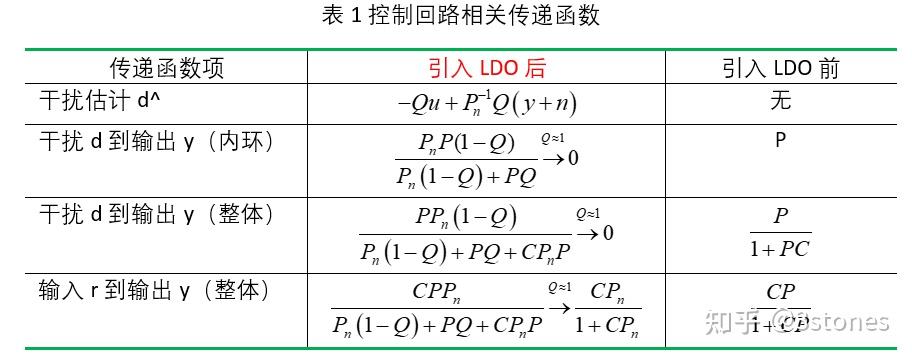
从表1中可以看出,滤波器Q的设计在LDOBC中起着至关重要的作用。理想情况下,在感兴趣的频率范围内,当Q(s)≈1时,LDO的引入带来以下好处:
- 无论是内环,还是外环,干扰d对输出y无影响,即干扰作用得以消除;
- 输入输出传递函数转变为标称模型Pn对应的传递函数,即可以标称模型设计控制器,标称模型和实际模型之间的差别得到完全消除;
以上优势使得DOBC的控制设计可以分别处理跟踪和抗扰,标称性能和鲁棒性能,大大简化了控制器设计过程。然而,在实际中,滤波器Q通常设计为低通滤波器,这一设计主要基于以下考虑:
- 低通滤波器Q与逆标称模型相结合,能够保证组合成的传递函数相对阶数大于0,以满足因果关系,在物理上可实现,在实际控制运算中避免代数环(参考图3);
- 对于实际物理系统而言,干扰一般为中低频(即使有高频干扰,考虑一般控制系统如机械运动系统体现为低通特性,高频干扰对系统影响也相对较小),传感器噪声为中高频。因此在设计滤波器时,一般要保证其截止频率要高于干扰频率,以保证干扰能够准确的被估计出来,但是同时又能够衰减高频噪声,以保证传感器测量噪声不会对干扰估计造成影响;
- 滤波器阶次、截止频率(带宽)的确定需要考虑多方面的影响,如被控对象特性(模型不确定、是否有延迟、是否稳定等)、干扰特性、测量噪声、鲁棒稳定性等多方面因素影响。因此,如果要合理干扰观测器,仍要掌握必备的时频域、(鲁棒)稳定性分析手段【6】【7】。
值得注意的是,为方便说明,图3假设被控系统为单输入单输出、非最小相位系统。实际中,对于非最小相位系统,通过改进观测器仍可以运用LDOBC改善系统控制性能。感兴趣的朋友可以参考综述文献【1】~【3】。
LDOBC与PID等效关系
如同LADRC(线性自抗扰控制)的低阶线性版本和PID之间等效关系【8】,低阶LDOBC也与PID也存在某种对应关系【9】【10】【11】。这种等效关系就为借助二自由度控制器能够分别处理跟踪和抗扰的优势,设计二自由度的PID控制器(即滤波+PID)奠定了基础,也帮助揭示了PID的抗扰机理和抗扰设计方法。
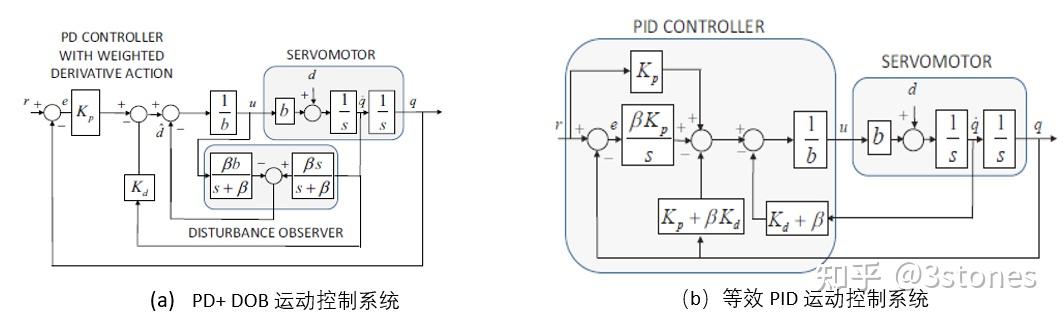
图4. PD+DOB与PID控制系统之间的等效【10】
如图4(a)所示,对于采用PD控制器的位置控制系统,为改善系统抗扰性能,设计一阶LDO(滤波器为一阶,带宽为beta),采用速度反馈和控制电流为输入。其等效系统如图4(b),LDO的引入,使得等效控制器含有了积分控制成分(原有控制器并不包含),且积分增益正比于观测器带宽,同时等效控制器的微分增益也随着LDO的带宽增加【10】。这清楚地表明了PID中积分的抗扰作用。类似地,采用比例+LDO的控制,也可以等效为PI控制【9】。
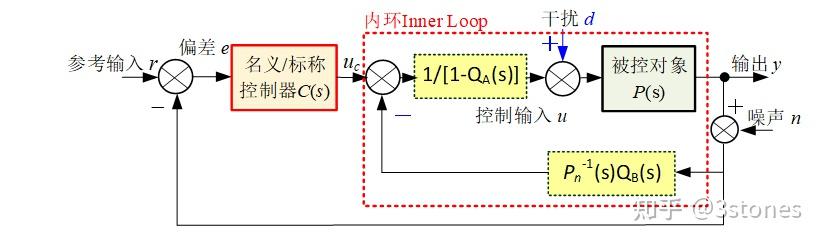
图5. LDOBC等效形式
LDOBC和PID之间的这种关系等效关系,可以用LDOBC(图3)的等效控制框图图5来说明。可以看出,滤波器Q的引入相当于在系统前向通道上增加了一个1/(1-Q)的传递环节,内环回路上增加了一个滤波函数。如果Q设计成为一阶滤波器,那么经1/(1-Q)变换后自然成为PI环节,比例增益为1,积分增益为观测器截止频率(滤波器为一阶时,截止频率就是带宽)。这一环节与原有PD控制器串联,本质上只是PID控制的一种体现形式:Kp(1+Ki/s)(1+Kds)。对于速度动态这个一阶系统来说,这一增加的反馈回路实际相当于不完全微分,反馈到控制输入端,因此,也相应的增加微分系数。值得注意的是,传统LDOBC中,滤波器Q只有一个。图5的等效形式表明,等效前向回路中的滤波器QA和内环反馈通道中的滤波器QB不必相同, 因此可以单独设计保证回路跟踪/抗扰性能以及反馈信号滤波【11】。
LDOBC的等效控制回路进一步为抗扰DR-PID控制器的设计奠定了基础,如图6所示。这种等效关系,为从系统期望闭环带宽(HR为期望闭环系统模型,用来替代名义/标称模型)、干扰观测器观测带宽以及系统相位补偿(Cpd)等控制系统频域性能直接整定PID控制和设计前置滤波函数奠定了基础。这一从二自由度控制器结构出发的PID参数设计方法已经在直流电机、移动机器人以及风行姿态控制中得到了应用,显示了优良的控制性能。感兴趣的读者可以参考聂教授课题组的知乎文章:PID控制器的抗扰原理(DR-PID)。
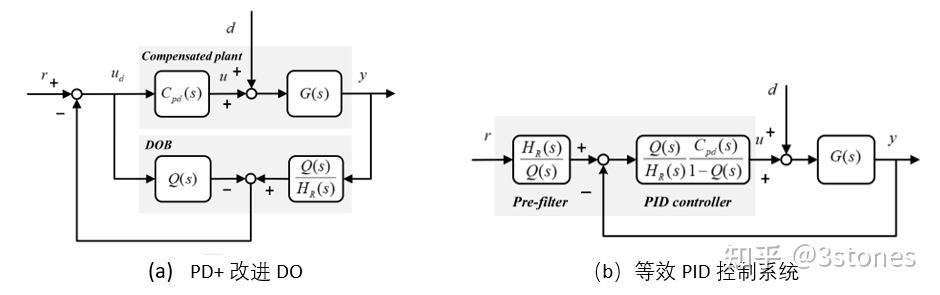
图6. 基于改进干扰观测器的抗扰PID【12】
从以上等效过程中可以看出,PID作为一种工程中最常用的控制器类型,目前关于其抗扰作用机理和相应的整定/设计方法仍未被完全揭示。无论从时域上理解的‘‘过去-现在-未来信息’’生成控制决策,还是传递函数上理解的‘’零极点对消或者相位超前滞后‘’视角在工程实际应用中仍然不够直观。从LDOBC等二自由度控制器出发无疑为揭示PID作用机理提供了视角。从PID反过来看LDOBC,根据内模原理IMP(Internal model principle),一般认为积分只能消除稳态干扰,既然LDOBC可以估计并消除动态干扰(在LDOB范围内即可),而且PID和LDOBC等效,那么回到PID中,这种消除动态干扰的能力(似乎与图5中的内环等效反馈回路有关)又能对PID的设计提供什么样的启发?另一方面,LDOBC忽略干扰的本身动态或者结构,只把干扰当成外在信号,与IMP的抗扰效果有多大区别(文献【13】提供了一种将IMP和DOBC抗扰思路相融合的方法,值得进一步研究)?基于IMP设计的PID控制器是否能够与LDOBC等效的PID控制器达到相同效果? 相信不同控制方法的互相启发能够为控制算法和控制实践的成熟奠定基础。
扩展:非线性干扰观测器NDO
对于非线性系统,利用频域分析、逆向标称模型设计干扰观测器的方法不再适用。因此需要回到时域状态方程的框架中,并采用类似状态观测器的方法设计NDO。考虑到非线性系统的多样性和复杂性,目前关于NDO的研究多集中在仿射非线性上(Affine nonlinear system,对控制是线性的,容易在控制输入端补偿观测的干扰),如图7所示。电液控制系统、机械臂控制系统等运动控制系统都可以归入到这一类。感兴趣的读者可以参考文献【14】,了解常见NDO的设计方法和在机械臂运动控制系统中的应用。由于参考文献已经写得相当简明,这里就不再重复了。
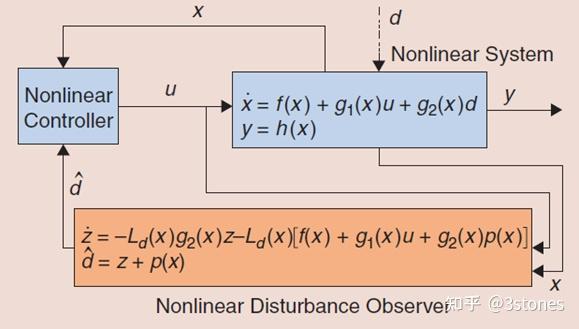
图7. 一种的常见的非线性观测器及其控制系统【14】
值得注意的是,NDO不像LDO,其稳定性能比较容易保证。NDO在控制系统中的引入,如同参数辨识模块在间接自适应控制中的引入,相当于给整个系统引入了附加动态,这部分动态的引入使得整个控制系统的动力学行为更加复杂。如果干扰观测器没有正确设计,观测出来的干扰远远偏离实际干扰,然后用不正确的干扰输入在输入端进行补偿(导致过补偿或者欠补偿),整个控制系统性能会下降甚至失稳。因此,必须首先通过稳定性分析和设计,确保干扰测误差动态能够有界(误差很小)或者趋近于0,然后在此基础上再次运用稳定性分析方法保证整个控制回路的稳定性。如同在‘控制算法手记-稳定性还是稳定性’所述,稳定性在先进控制算法的设计和控制系统的分析中发挥基础性作用。
总结
DOBC采用先估计未知干扰再补偿/衰减影响的思路无疑是处理干扰的一种有效方法。与此同时,还存在着诸如自适应前馈/反馈(Adaptive feedforward/feedback)、滑模(Sliding mode)、内模原理(Internal Model Principle)、H2/H无穷 等各种方法。即使是依托于观测器的干扰抑制,除了DOBC,也还存在着ESO/GESO、滑模(Sliding mode)、高增益(High-gain Observer)、UDE(Uncertainty and disturbance estimator)等各种方法。从本质上理解这些抗扰控制方法的基本思路是非常重要的,不仅能够避免工程师陷入各种控制算法的概念里,帮助工程师直面问题本质,正确的设计控制算法,而且还可以从更具物理直觉(Physical-intuitive)的视角加深对控制算法的理解。在面临实际控制问题时,切忌照搬各种算法或者控制理论,纠结于哪个工具好用,而是要先搞清楚自己的问题是什么(比如干扰从哪里来,本质上什么导致的,怎么影响系统,干扰信息或者结构是否可知等),目的是什么,建立以控制性能目标为导向的控制算法设计观念,然后再选择合适的工具或者工具组合,最后再研究如何把工具用好,或者对工具进行优化。同其他文章类似,本文并不会深入DOBC的细节,感兴趣的读者可以参考相关文献或者翻阅下面的专著进行深入学习。

图7. 关于DOBC的专著
【参考文献】
1. W. H. Chen , J. Yang, L. Guo and S. Li, . (2016). Disturbance-observer-based control and related methods—an overview. IEEE Trans. Industrial Electronics, 63(2), 1083-1095.
2. E. Sariyildiz, R. Oboe and K. Ohnishi, (2019). Disturbance observer-based robust control and its applications: 35th anniversary overview. IEEE Trans. Industrial Electronics, PP(99), 1-1.
3. J. Yang, W. H. Chen, S. Li, L.Guo, and Y. Yan, . (2016). Disturbance/uncertainty estimation and attenuation techniques in pmsm drives–a survey. IEEE Trans. Industrial Electronics, 64(4), 1-1
4. J. Su, W. H. Chen and J. Yang (2016). On Relationship Between Time-Domain and Frequency-Domain Disturbance Observers and Its Applications. J. Dynamic Sys., Meas. Ctrl., ASME.
5. K. Ohishi, K. Ohnishi and K. Miyachi, (1983), Torque-Speed Regulation of dc Motor Based on Load Torque Estimation. Proc. IEEJ IPEC-TOKYO, 2, pp.1209–1216.
6. E. Sariyildiz, and K.Ohnishi, (2014). A guide to design disturbance observer. J. Dynamic Systems, Measurement and Control, Transactions of the ASME, 136(2), [021011]
7. E. Sariyildiz, S. Hangai, T. Uzunovic, T. Nozaki and K. Ohnishi. (2020). Stability and robustness of the disturbance observer-based motion control systems in discrete-time domain. IEEE/ASME Trans. Mechatronics, PP(99), 1-1.
8. H.Jin, J. Song, W. Lan and Z. Gao, (2020) On the characteristics of ADRC: a PID interpretation. Science in China Series F:Information Science, vol. 63, no. 10.
9. L. Luna, and R. Garrido, . (2018). On the equivalence between P+DOB and set point weighted PI controllers for velocity control of servo-drives under load disturbances. Congreso Mexicano de Robotica.
10. R. Garrido and J. L. Luna. (2018). On the equivalence between PD+DOB and PID controllers applied to servo drives. IFAC-Papers OnLine, 51(4), 95-100.
11. H. Shim, G. Park, Y. Joo, J. Back and N. H. Jo. (2016). Yet another tutorial of disturbance observer: robust stabilization and recovery of nominal performance. Control Theory and Technology.
12. ,Z. Y. Nie, C. Zhu, ,Q. G. Wang, Z. Gao, and J. L. Luo. (2020). Design, analysis and application of a new disturbance rejection pid for uncertain systems. ISA Transactions, 101.
13. Y. Joo, G. Park, J. Back and H. Shim. (2016). Embedding internal model in disturbance observer with robust stability. IEEE Trans. Automatic Control, 61(10), 3128-3133.
14. A. Mohammadi, H. J. Marquez and M. Tavakoli. (2017). Nonlinear disturbance observers: design and applications to Euler-Lagrange systems. IEEE Control Systems, 37(4), 50-72.
15. S. Li, J. Yang, W.-H. Chen, and X. Chen, Disturbance Observer based Control: Methods and Applications. CRC Press, 2014. |
|